СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ИЗМЕНЕНИЯ НАДЕЖНОСТИ ЛЕТАТЕЛЬНЫХ КОМПЛЕКСОВ ПРИ ОТРАБОТКЕ И ЭКСПЛУАТАЦИИ

Рассмотрим методику статистическо­го оценивания функций изменения надежности объекта. В § 4.3 были получены модели изменения надежности, с помощью которых через

неизвестные параметры описывалось изменение функции надежности при проведении доработок.

Задачу статистического оценивания функции (4.55)

Р* = Р«, — (Р» ~Р0) ГЇ (1 — akjР^)

можно решить, если будет установлен закон распределения оценки

Л

Pt для всех i = 0, 1,2, …

В практических задачах часто можно ограничиться нахождением

Д

оценки функции Pt и ее дисперсии а2[Р;1 = о,2, принимая закон рас-

А

пределения оценки Pi близким к нормальному. Для этого в первую

Л Л Л

очередь необходимо найти оценки а, Р0, Р«, параметров а, Ро, Рос и их ковариационную матрицу: *

и р — соответствующие коэффициенты корреляции оценок.

Л Л Л

Если найдены несмещенные оценки а, Р0 и Р^, то, пренебрегая не­линейностью зависимости функции (4.55) от параметров, несмещенную оценку функции можно получить в виде

Л ‘ Л Л Л «■ Л Л

Pi = Poo — (Рсо — Р„) П (1 — СЛ./Р»). (5.177)

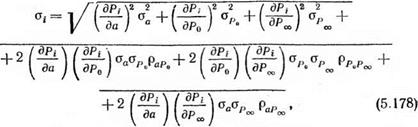Среднее квадратическое отклонение этой оценки как линеаризо­ванной функции от трех случайных параметров может быть вычислено по известной ковариационной матрице (5.175):

где частные производные функции PL по соответствующим параметрам

АЛЛ

вычисляются при а — а, Р0 — Р0, Рте= Р™.

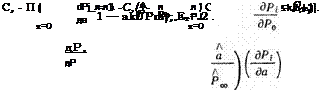Выражения для определения частных производных в соответст­вии с (4.55) можно записать в следующей компактной форме:

Полагая, что закон распределения оценки функции Pt в каждом і-м сечении — нормальный со средним квадратическим отклонением (?г, нетрудно рассчитать в соответствии с (5.83) или (5.84) двусторонний или односторонний доверительный интервалы при доверительной вероятности у(уі):

Заметим, что в данном случае пренебрегаем разницей между оцен-

Л

кой дисперсии о? и неизвестным истинным значением о2. В принципе, используя распределение Стьюдента, можно по выражению типа (5.35)

Л Л

найти и более точный доверительный интервал Р,—t-Xikoi<Pi<, Л Л

< Pi + t-t’kOi.

Л Л Л

Рассмотрим методику определения оценок й, Р0, Р0о и ковариацион­ной матрицы (5.175). Для использования того пли иного метода стати­стического оценивания необходимо решить вопрос о зависимости или независимости результатов испытаний, по данным которых будут опре­деляться оценки.

Представим щ — число испытаний между (< — 1)-й и і-й доработ-

Л

ками; ті — число отказов в nt испытаниях; kt — количество устраняе­мых в і-й доработке причин отказов в зависимости от номера доработ­ки в следующем виде:

Результаты испытаний внутри каждой группы можно считать не­зависимыми, полагая, что До внесения доработки объекты и режимы испытаний остаются неизменными. Исходы испытаний между группа­ми, разделенными доработками, строго говоря, зависимы. Это связано

с тем, что по данным испытаний предшествующей группы проведена доработка, которая меняет величину надежности, а следовательно, влияет на исходы испытаний в последующей группе. В работе f 17І показано, что зависимость между группами испытаний слабая и ею можно пренебрегать.

Л Л Л

Суть задачи отыскания оценок а, Р0, Р<» заключается в расчете та­ких параметров модели (4.55), при которых оценка функции (5.177)

Л л

наилучшим образом прилегала бы к опытным точкам Рг = 1 —т^щ. Сложность решения задачи состоит в том, что на практике значения

Л

Пі обычно малы и часто щ = 1. При этом опытные точки Рг будут при­нимать значения 0 или 1. Следовательно, нужно найти вид функции (5.177), которая бы наилучшим образом аппроксимировала опытные

д

точки Pi, чаще всего находящиеся на пределах диапазона изменения.

А Л *t

В этих условиях для получения оценок а, Р0, Рх и матрицы (5.175) может быть использован. метод максимума правдоподобия.

Л

Число отказов тх в nt независимых испытаниях имеет биномиаль­ное распределение (5.10) с вероятностью

Л Л А / л л

вер (гщ) = ПіРПі т{ (1 — Рі)ті I (nt — rrii)! Ші!.

Функция правдоподобия для всей выборки, представленной дан­ными на с. 208, в соответствии с (5.11) при условии независимости меж­ду группами испытаний принимает вид

Используя модел’ь (4.55), получим функцию правдоподобия, за­висящую от искомых параметров:

L (Pt (а, Р0> Рсо)) — п д д |Роо (Рею Ро) П f 1 ~

1=0 («г — щ)! mi! L s=o

Перейдем к логарифмической функции правдоподобия, опуская по-

/Г л А

стоянный множитель ПіМЦщ — m,)!m£!l, не влияющий на положение максимума:

In L (а, Р0, Р«,)= І j(«i — in,) In Гр» — (Poo — P0) П (1

і■—o L s=0

j+ т! Іп[і-P00+(P00-Po) П fl—^-) }• (5.183)

Можно показать (см. (І7І), что функция InЦа, Р0, Р°°) имеет единст­венный минимум в точке

V [—InL(a, Р0, Ра0)1 = О,

являющийся решением системы уравнений правдоподобия

ajn_L=0; ii! LL = 0; 4^=0. (5.184)

да дР0 ’ дР„ >

(5.185)

При этом искомая матрица (5.175) является обратной отрицательной от (5.185):

В = —А-‘. (5.186)

АЛЛ

Таким образом, для определения оценок с, Р0, Рх необходимо най­ти минимум выпуклой функции — InL (а, Р0, А») (см. (5.183)1, завися­щей от трех переменных, а для расчета ковариационной матрицы вы­числить обратную отрицательную матрицу вторых производных функ­ции InL (а, Р0, Рос). Решение подобных задач на ЭВМ не представляет трудностей, так как соответствующие программы поиска минимума выпуклой функции и обращения матриц входят в математическое обес­печение машин.

Кроме исходных данных, представленных на с. 208, необходимо

АЛЛ

найти нулевое приближение а(0), Р<0), , позволяющее начать реше­

ние задачи поиска минимума функции —lnL(a, Р0, Рх). Рассмотрим один

АЛЛ

из вариантов нахождения величин а<0>, Р<°>, Р£). Как отмечалось выше, величина Рос обычно близка к единице, поэтому можно принять

Л Л

= 1. Значение Р<°> находят по результатам первых I — 5 — 10 испытаний как оценку

А ґ’к <п А

Pol = ро = 1 — ЩІІ. (5.187)

л,

где т, — число отказов в первых / испытаниях.

Л

Для вычисления величины п(0) используем следующий прием. По результатам последних г — 5 — 10 испытаний из п проведенных найдем оценку функции надежности в п-м сечении:

Л Л

Pnr= 1 — тг/г.

Среднее значение числа устраняемых причин отказов в одной доработке

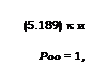*=(!/>) 2 kt.

1=1

При условии, что в каждой доработке величины kг из (4.55) для сечения п получим

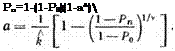откуда

(5.190)

Подставляя в (5.190) вместо истинных неизвестных значений Р0 и

Л ’ Л ». Л

Рп оценки Ры из (5.187) и Рпг из (5.188), найдем оценку а1г как ис­комую нулевого приближения:

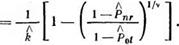(5.191)

Нетрудно заметить, что оценка Ры из (5.187) дает несколько завы-

Л

шенное значение оценки Р0, так как возрастающая функция Рг = Р} на интервале (0, I) заменяется средним значением (рис. 5.9). Анало-

л

гично можно показать, что оценка Рпг по (5.188) несколько ниже зна — Л л

чения Рп. Следовательно, и нулевое приближение а1г в (5.191) дает

Л

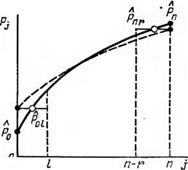заниженное значение а, описывающее медленнее растущую функцию, показанную на рис. 5.9 пунктиром. Из структуры функции (4.55) видно, что рост надежности воз­можен лишь при условии, когда

Л Л

1—akilPoo> 0 (/=1,2,…, v), откуда

Л Л

acPJikJ шах ^ і m шах • l<t<v 1 /<V

(5.192)

С учетом сказанного можно сузить области поиска минимума функции —InL(a, Р(), Poo) с помощью следую­щих неравенств:

1W max >

l<i<v

л 0<Р„	р( 0) м>	л л Рпг ^ Роо ^

 

Приближенное значение среднего квадратического отклонения

л

о1Рп] == ап оценки функции надежности при отсутствии данных о ковариационной матрице (5.175) может быть найдено по формуле (см. І17І)

о„ = (0,8 ч — 0,9) VРЛ1 — Рп)1п, (5.193)

А »

где Рп — оценка функции в сечении / = п ; п = ^ «і — общее коли­

ві

чество испытаний.

Пример 5.26. Пусть в результате летной отработки ЛА получены исходные данные:

і. .	. • >	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
Пі, Л	, . .	2	1	1	1	1	1	1	1	1	1	1	1	1	2	1	6
ті.		1	0	1	1	0	1	0	1	1	1	0	0	0	0	0	2
ki.	, . ,	0	1	5	2	1	2	4	1	1	6	2	2	1	2	1	1

Найти оценки функции Р; и Pj надежности ЛА по данным летной отработки. В соответствии с приведенными выше данными общее количество испытаний

л = 2 пі = 23;

£=!

А ’ А

общее количество отказов т = ^ mi = 10; общее количество доработок v = 15; среднее количество устраняемых причин отказа в одной доработке

k — — Іі *г = 2,133.

V £=1

Убедимся, что при данных результатах испытаний имеет место изменение надежности. Если считать все результаты испытаний как отражение какой-то средней надежности ЛА, то биномиальная оценка (5.12) имеет следующее значе — А А

ние: Pg=l — mlп — 1 — 10/23 = 0,565; ее среднее квадратическое отклоне­ние (5.13) будет с [Pel = °б = V^Pc ( 1 — Рб)^(п — 1) = V 0,565 (1 — 0,565)/(23 — 1) =0,1057.

_ Л

В этих условиях, полагая, что оценка Рр имеет близкое к нормальному рас-

л

пределение (Ре далеко отстоит от 1), построим двусторонний доверительный ин­тервал (5.83) оценки при коэффициенте доверия у = 0,9:

Л Л

рб — ц1+т °С < Рб < Рб + «1+т о«).

2 ~

тогда 0,565—1,645 • 0,1057 < Рб < 0,565 + 1,645 • 0,1057, или 0,391 < Рб< < 0,739.

В предположении, что изменение надежности существенно, вычислим оцен­ки нулевого приближения а*0) и Р*{^. По (5.187) и (5.188) найдем оценки по пер-

Л л

вым пяти и последним девяти испытаниям: Р0[ = 1 — 4/5 = 0,200; Pnr = 1 — — 2/9 = 0,778.

Л

Таким образом, отклонения оценок от среднего значения Яр = 0,565 вы­ходят за доверительный интервал (0,391; 0,739) и должны рассматриваться как существенные, свидетельствующие о наличии изменения надежности в ходе от-

л

работки И необходимости построения оценки функции РI- С учетом этого вычис­лим по (5.191) нулевое приближение параметра а:

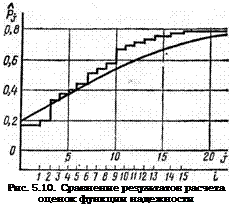
Построим график оценки функции надежности при нулевом приближении оценок параметров (кривая на рис. 5.10):

В сечении / = п (i = v) получим Рп = 0,759.

По (5.193) вычислим в сечении п среднее квадратическое отклонение оценки функции:

о„ = 0,85 У 0,759(1 —0,759)/23 =0,076.

Для оценки Рп при к = 0,9 и в предположении нормального распре­деления оценки в соответствии с (5.83) доверительный интервал

0,759 — 1,645 • 0,076 < Рп < 0,759 +

+ 1,644 ■ 0,076,

или 0,638 < Рп < 0,884.

Расчет оценок максимального

Л Л Л

правдоподобия а, Р0, Рсо на ЭВМ минимизацией функции lnL(a, Р0, Роо) [см. (5.183)] по алгоритму, опи­санному в [17], дает следующие ре-

Л л

зультаты: а = 0,0367; Р0 = 0,172;

Роо= 0,977; р’„= 0,763 и оп = 0,077. График оценки функции

А А /А А 1 1 P»=Pco4Pco-Po) П Iі	А А — aks/P со) =
&=0
і = 0,977 —(0,977 — 0,172) П (1-	-0,0367*^/0,977)
5=0
представлен ломаной на рис. 5.10.

В сечении / = n(t = v) при y — 0,9 в предположении нормального распре —

Л

деления оценки (5.83) двусторонний доверительный интервал оценки Рбудет
0,763—1,645 • 0,077 < Рп < 0,763+ 1,645 • 0,077,
или 0,636 < Рп < 0,884.

Заметим, что даже нулевое приближение в данном примере достаточно точ­но описывает начало и конец процесса, хотя в некоторых точках расхождение значительно.

Использование метода максимума правдоподобия позволяет ре­шить задачу в общем случае, когда tti малы или равны единице. Если же Пі > Ю ~ 20 и число точек і = 1,2, …, v (v ;> 10), то можно

Л Л Л

для определения оценок а, Р0 Рх и ковариационной матрицы (5.175)
использовать частный случай метода максимума правдоподобия — ме-
тод наименьших квадратов. Такой переход (5.23) соответствует допуще-

Л л

нию о нормальности распределения оценок Pt — 1 —трщ.

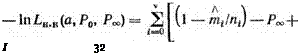Если принятое допущение справедливо, то отрицательная функция правдоподобия (5.23) в условиях рассматриваемой задачи запишется:

+ (Р„ — Р0) П (1 —akJPoo) ■

s=0 J

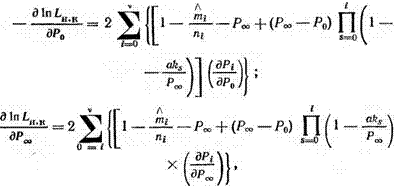Нормальные уравнения (5.24) в соответствии с (5.194)и принятыми обозначениями (5.179) могут быть получены следующим образом:

откуда запишем:

[(£.-n)/£ji(^A£.) = 0; s(spa) = o:

s {sp, [l — С, (l — ї /pj[(p„ — Р.) /pj C, E,]} = 0, где 8Pj = 1 — mjrii — Poo + ^PTO — P0J П (^1 — akJPoo J.

При использовании метода наименьших квадратов нулевое при-

Л л

ближение можно найти, принимая Лі = £иР00=1. В этих условиях функция (4.55) принимает вид

Рг = 1 —(1 —Р0)(1 — dfy. (5.196)

После замены обозначений типа (4.58)

3 = —1п(1 —ak) (5.197)

функция (5.196) может быть записана в виде

Pi = 1 — (1 — Р0)е-Эг. (5.198)

Введя обозначения

1п(1 — Pt) = Уі; ln(l — Р0) = А, (5.199)

представим функцию (5.198) в следующей форме:

Уі — А — Зі. (5.200)

Таким образом, получили линейную функцию yt относительно ар­гумента І, для которой в соответствии с (5.25) нормальные уравнения могут быть записаны в виде

І] (уі + Зі ~ А) і= 0; у (уt + 3t[— А) = 0. (5.201)

і=і й

Уравнения (5.201) легко разрешаются относительно неизвестных

л л

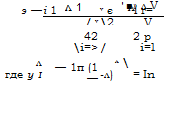оценок А и Э:

С учетом обозначений (5.197) и (5.199) нулевые приближения при­нимают вид

Рассмотренная выше последовательность расчета оценок парамет­ров моделей изменения надежности методом наименьших квадратов может быть использована и при оценивании обобщенного показателя надежности ЛК по результатам эксплуатации. Предложенная в § 4.1 упрощенная модель изменения надежности 1см. (4.77)1

_ 97

1-(1-Я10)е * (5.204)

содержит два неизвестных параметра Rl0 и Э, которые могут быть оце­нены методом наименьших квадратов, если известны нормально рас-

А

пределенные точки Ri. Обычно достигнутые к моменту эксплуатации tt значения Ri обобщенного показателя надежности ЛК оцениваются

А

по большому объему информации и можно считать оценки Rt распре­деленными нормально. Тогда, вводя обозначения, аналогичные (5.199), из (5.204) получим:

z(tl) = zi = Ai-3ti г, = In[1—/?&)]; At = ln(l — R10). (5.205)

Используя выражения (5.202), после преобразований получим искомые оценки параметров Л4 и Э:

(5.206)

i=l

i=l

где t =

По аналогии с (5.203) найдем

А

А. Я, Rio ~ 1 ® •

Для определения ковариационной матрицы при использовании ме­тода наименьших квадратов нужно по функции правдоподобия (5.194) вычислить значения матрицы ее вторых частных производных (5.185), а затем в соответствии с (5.186) найти и саму матрицу В.

Для случая, когда функция надежности содержит только два параметра и после преобразований сводится к прямой типа (5.205), можно предложить известный метод построения доверительной облас­ти на оценку линейной функции, найденную по методу наименьших квадратов.

Суть метода, изложенная в работе [7І, состоит в следующем. Пусть

Л Л

методом наименьших квадратов находят оценки а и b параметров а и Ь прямой у — а (х — х) + b по п независимым нормал ьно распре-

л — 1 "

деленным наблюдениям (yt, х;) на интервале с < х < d, где х = —2**’

i = l

В соответствии с теорией метода наименьших квадратов оценки находят по следующим формулам:

П

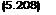д У і (х*

‘ (=1

S(*I — 1=1

Л _

Тогда для оценки а(х — х) + b доверительная область с коэффи­циентом доверия у на заданном интервале (с, d) определяется функция­ми

Л Л /" — Л Л

#1в (н) (А) = а х~ х) + Ь ± а у (х, у);

А у (х, у) = wn_2 (7, I) S (х — х)2 / 2 (м — *)2+1 /«•

Величины, входящие в функцию Ау(х, у), вычисляют по следующим выражениям:

-* [ 2 Л Л. —. Л

S=y 1 /(п — 2) 2 є.; е yi — a(xl — x) — b;

С=(с —х)/]/ х)2 * (5.210)

0= (d-l)/]/І (л-,-*)2 ;

Л- = Т 0.5 11 — (1 + пС£>)/)/(1 + пС2) (1 + nD2)] •

Функцию ц„_2(у, Я.) находят из табл. П.13 по входам п— 2, X

Л

при у = 0,90 и 0,95 (см. 17І). Можно показать, что функции уів(н)(х) [см. (5.209)1 являются гиперболами, расходящимися от сечения х — х.

В нашем случае, когда изменение обобщенного показателя надеж­ности ЛК на этапе эксплуатации описывается функцией

R(t)= l-(l-tfi0)e~3<, (5.211)

вводя обозначения

п

х — tі х — — t^ = t і с — , d = tn,

1ST

b = —ln(l —Ri0); a = —Э; y(x) = In [I — #(*)] + 9t,

можем перейти к прямой у(х) = а(х — х) + Ь, а следовательно, вос­пользоваться приведенными выше зависимостями (5.209), (5.2Ю).

Оценки Э и Ri0 могут быть найдены по зависимостям (5.206) и (5.207),

если заданы опытные значения Rit tit которые с учетом принятых обоз-

Л

начений трансформируются в опытные точки yit хі.

С учетом принятых обозначений (5.212) можно записать

у = ln(l — R) + ЭТ. (5.213)

Продифференцировав обе части выражения (5.213) и перейдя к конечным отклонениям, получим:

dy = d [In (1 —R) -{-9t J;

dy = —dR/{l—R)-, Др=— ДЯ/(1 — R). (5.214)

С учетом (5.2І4) можно записать выражения для функций, ограни­чивающих доверительную область оценки

. Л Л

А А

R(t)=-(l-Rl0)e :

± AR (t, у) = =F [ 1 — і? (01Ау (t, V), (5.215)

откуда окончательно имеем выражения для функций, ограничивающих снизу (сверху) доверительную область с доверительной вероятностью у:

к (в) (*, У) = 1 — (1 — Ri о) е~3′ =F (1 — ко) А У (t, Y). (5.216)

Пример Б.27. Пусть по результатам пяти лет эксплуатации ЛК получены

А

оценки Ri обобщенного показателя надежности, представленные ниже:

і…………… 1 2 3 4 5 6 7 8 9 10

ti, годы. . 0,5 1,0 1,5 2,0 2,5 3,0 3,5 4,0 4,5 5,0

А

Ri…………. 0,50 0,57 0,70 0,70 0,68 0,80 0,77 0,75 0,87 0,88

Найти оценку функции обобщенного показателя надежности и ее двусторон­ние доверительные пределы при коэффициенте доверия К = 0,90.

Результаты расчетов параметров, входящих в (5.206), (5.207), (5.209) — (5.216), сведены в табл. 5.2.

В соответствии с данными табл. 5.2 при v = п и = ln(I — Rj) по (5.206) и (5.207) находим оценки параметров:

2 *г1п(1-І? і)-ТІ; 1п(1-Д,)

Э= ±±_________________________________ =

nb-j U

i=1

— 43,555 — 2,75(— 13,710)

——— : “ ———- L 3s 0,2837 « 0,284;

10 • 2,752 — 96,25

п

Л 1 л л-

Ai = — 2j ln О ~Ri) + 3t =

<=і

= — (— 13,710) + 0,284 ■ 2,75 = 0,5913 да 0,591;

—ІQ.69I „ .

■е =0,446.

Таким образом, оценка функции имеет вид (сплошная линия на рис. 5.11)

R(t) = 1 — (1 — 0,446) е*~°’284 *. Найдем функции, определяющие доверитель-

. А

иую область оценки /?(<); для этого по (5.210) с учетом данных табл. 5.2 и обоз­начений (5.212) вычисляем:

S= £? /(п —2) = Vl • 0,2643/(10 — 2) =0,1818;

С = (tt —1)I / 2] (ft — Г)2 =40,50 — 2,75) /у 20,625 = — 0,4954;

D = (tn~t)jy 2 0j-

л

Я

Л=Ко,5 (1 —(1 +nCD)/ V(l+ nC2) (1-f n№)] =

= 1^0,5 {l — [l + 10 (—0,4954) 0,4954]//[1+10(—0,4954)2][1+10-0,4954*]) =

= 0,8429,

где ег = In (1 —Ri) + 9t — Э (ft — t) + In (1 — R10) = In (1 — R10) + 3ft +

+ In (I —RA­TIO табл. П. 13 при у = 0,9, n —2 = 8, Я = 0,8429, интерполируя, находим н8(0,9; 0,8429) = 2,449.

В соответствии с (5.209) и данными табл. 5.2 находим

± Дy(ti) — ±"n-a(T. *)$

= ±2,449 • 0,1818 V (ft -2,75)2/20,625 + 1/10 •

На основании (5.216) получим искомые функции нижнего и верхнего пре­делов доверительной области:

‘;) = 1 — (l —Rl0j Є «ю)е Э‘лy(ti).

Л Л

Функции Ян(в) (ft) (пунктирные), R(t) (сплошная) и опытные точки Rt пред­ставлены на рис. 5.11,